My previous two points provided an example of how even internationally regarded scholars can blunder badly when they stray outside of their sphere of competence. Needless to say, when a layperson with zero professional training, expertise, or experience in a technical discipline declares that the entire discipline is fraudulent or not 'true science', no one outside of the echo chamber of those who agree with that person's assertions on ideological grounds will take his assertions seriously.
Unfortunately, this problem is endemic in our community, where laypeople without any scientific training at all will nonetheless claim that robust, long-standing positions in the scientific community on the age of the Earth, or common descent are false. The burden of proof lies solely on the person making such a novel claim, and personal opinion leavened with a few claims taken uncritically from special creationist websites, and advanced on an internet forum hardly counts as a definitive refutation. As vertebrate palaeontologist Per Ahlberg put it when responding to a special creationist:
OK, fine, if that's what you think, why don't you marshal your arguments into a paper and submit it to a scientific journal? I'm serious: the Intertubes is all very well for discussing ideas in a general way, but if you have a real scientific point to make you need to get it out in the form of a proper paper in a peer-reviewed journal. Otherwise it won't be taken seriously.
One searches the professional peer reviewed literature in vain for papers published by Christadelphian special creationists that have made a "real scientific point" and have been able to gain considerable scientific support for their view that the Earth is 6000 years old and common descent false. Given this, it is quite reasonable, as Ahlberg would put it, not to take such Christadelphian YEC claims seriously as they are not even wrong.
A few years ago, I saw the following on a now-defunct Christadelphian forum:
A few years ago, I saw the following on a now-defunct Christadelphian forum:
The fact that the earth is 4.5 billion years old is not well established. It is a belief. Dating based on radiocarbon dating and radioactive decay is seriously flawed, and anybody who doesn't look again at the dating methods isn't treating the subject seriously enough. Honestly"
The author, who was definitely not a geologist, geochemist, palaeontologist, or geophysicist provided no robust evidence to defend such a claim, one that over a century ago would have been regarded as misled at best by mainstream Christadelphians such as second editor of The Christadelphian, C.C. Walker:
Ten years ago the average scientist would have asserted that our habitable globe had not existed for more than a hundred million years. Now it would be hard to find a competent physical specialist who would fix a definite maximum below a thousand million years: [1]
Since then, the age of the Earth has been fixed at around 4600 million years; C.C. Walker would find it almost impossible to find a "competent physical specialist" who would argue for a 6000 year old Earth. Here's why:
1. Background theory
Let's look at the basic maths behind radiometric dating which involves nothing more onerous than first order differential equations. While I appreciate that there are many math-phobic people out there, by looking at the basic principles, I hope to show the interested reader the fundamentals behind radiometric dating, and also show that the YEC who asserts that radiometric dating is false, but cannot even master basic algebra is hardly in a position to be taken seriously.
Consider a radioactive element. The rate of decay is proportional to the number of radioactive atoms present:
dN/dt = -λN
which when differentiated gives N = No exp(-λt). No is the initial number of radioactive atoms, N is the current number of radioactive atoms and λ is the decay constant (the probability that any nucleus will disintegrate in the time dt. The mean life τ is the recipriocal of λ, and this allows the decay equation to be written as N = No exp(-t/τ) The half life by definition refers to the amount of time for half the isotope to decay to decay: By substitution, 0.5 = exp(-t/τ); ln(0.5) = -t/τ and finally, t = 0.693τ.
In practice, radiometric dating can be fairly complicated, but the underlying principle is fairly simple: knowing the decay constant of an isotope, the current amount of that isotope and the amount of decay product, we can calculate the date of origin of the rock.
YEC assertion: decay constants vary.
Response: No they don't - not to the degree that YECs claim they do. If decay constants varied at a rate fast enough to allow a young earth, the crust of the Earth would have melted from the accelerated release of heat and any life on Earth would have been sterilised to oblivion from the ionising radiation released.
In fact, we have direct observational evidence confirming that decay constants have not varied over thousands of millions of years. Supernovae observations have also confirmed that radioactive decay constants do not vary to the degree YECs claim they do. As a result of supernova nucleosynthesis, each supernova results in the production of isotopes which each have characteristic gamma radiation emission frequencies and fading rates; these are a function of their known decay constants. We have measured these characteristic gamma emissions from supernovae 170,000 light years, 60 million light years and several thousand million light years distant. The light from these supernova has taken between 170,000 to several thousand million years to reach us, which means that the decay constants have not varied over the life of the earth. [2, 3] The YEC claim that decay constants vary is false
2. Radioisotope dating principles
If a rock crystallises, trapping Nr atoms of isotope r, and the box remains a closed system (there are ways of determining whether a system has remained closed, contrary to what YECs claim - it's rather insulting to claim that professional geochemists are so stupid that they fail to allow for this contingency), then we can calculate the numbner of atoms of isotope r at time t by the following equation:
Nr(t) = Nr(0) exp (-λt)
where Nr(0) and Nr(t) are the amounts of isotope r at times 0 (formation or rock) and t, and λ is the decay constant.
Rearranging terms gives:
t = (1/λ) ln [ Nr(0)/Nr(t) ]
While we cannot directly measure Nr(0), the number of radioisotope atoms at the time of the rock formation, this can be overcome by using parent-daughter isotope dating methods. Nd(t) and Nr(t) are the numbers of atoms of daugher isotope and parent isotope respectively.
Recall that Nr(t) = Nr(0) exp(-λt). Now: dNd(t)/dt = -dNr(t)/dt = λ Nr(t). As Nr(t) = Nr(0) exp(-λt), the rate of change of daughter isotope with time is: dNd(t)/dt = λNr(0) exp(-λt). By integration: Nd(t) = -Nr(0) exp(-λt) + C.
Recall from elementary calculus that you can obtain the constant C by setting t to zero and suibstituting in Nd(0), C = Nd(0) + Nr(0). Substitute this into the equationm for Nd(t) and we get:
Nd(t) = Nd(0) + Nr(0) * (1- exp (-λt).
As Nr(0) = Nr(t) exp(λt). we can eliminate the unknown term Nr(0) and arrive at the following:
Nd(t) = Nd(0) + Nr(t) [exp(λt -1]
Now, if the rock has remained a closed system, and we know the values of Nr and Nd, we can calculate t if we know the number of daughter atoms at time zero. Solving for gives the equation:
t = (1/λ) ln [ (Nd(t) - Nd(0)/Nr(t)) + 1]
In practice, the value Nd(0) can be estimated or ignored, allowing the age of the rock to be calculated.
3. Compensating for possible errors in radiometric dating - concordance and isochrons.
The dating methods work if the amount of daugher element at the time of rock formation is known, can be inferred or ignored, and if we know that the system has been closed, preventing parent and daugher element from entering or leaving the system.
One way of verifying these ages is the concordant / discordant age approach. If one measures the radiometric ages of different minerals in a rock sample using method X, and all the radiometric ages agree, then our confidence in the validity of the age increases. In reality, the criteria for determining concordance are fairly stringent, in order to guarantee that the likelihood of the age being reliable being high.
The isochron dating approach is largely independent of these problems, and has proven to be quite useful in reality. This requires us to measure the parent elements, its decay product, and a non-radiogenic isotope of the daugher element to be measured. A number of samples are taken from the rock, and plotted on a graph where the X acis is the ratio of parent element to radiogenic daugher element [r/di], and the Y axis the ratio of the non-radiometric daugher element to its radiometric isotope [d/di]. The idea behind this method is to see if there is any relationship between the level of parent element (the independent variable) and any enrichment of the daugher element (the dependent variable).
For those who have studied chemistry , you will remember that isotopes still have the same basic chemical property, meaning that at the time of rock formation, the minerals in it would inherit the same ratio of non-radiometric daugher element to its radiometric isotope, which means that for a rock at time zero, if we take multiple samples, then they would all have the same ratio of non-radiometric daugher element to radiometric daugher element (remember that none of the parent element would have decayed into the daugher element at time zero). A plot of [d/di] against the independent varuiable [r/di] is a straight line of slope zero with the y intercept the initial ratio of non-radiometric daugher element to the radiometric isotope.
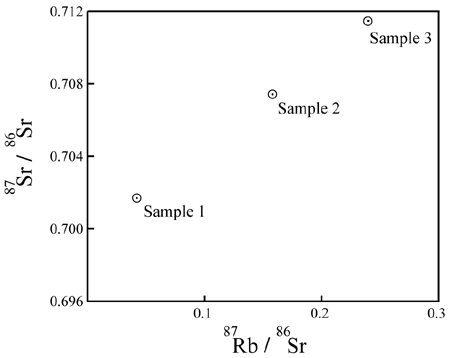 |
| Sample Isochron Plot. Source: Chris Stassen "Isochron Dating" |
The avidity with which minerals incorporate parent element varies, so for time 0, as one moves in a positive direction along the x axis, you will find the sample points corresponding to mineral samples that incorporate the parent element with greater ease than the daughter element. This explains what we would expect with the isochron at time zero.
Now, as the sample ages, the parent element will decay to the daughter isotope. For each of the original sample points in the rock, the amount of parent element r will decrease which the amount of radiometric daugher isotope di will increase. Remember that decay takes place in a proportional manner, so the larger the amount of parent element, the the greater these data points will move. If we plot these lines over time, what we see is that the data points remain colinear and the slope increases. These straight lines are isochrons, and they can be used to determine the age of the sample. As the respected geologist Claude Allègre points out, with respect to the RbSr dating method:
"Let us take the example of a series of minerals (or total rocks) which are assumed to be cogenetic (minerals from the same rock, or rock from the same massif). The 87Sr/86Sr and 87Rb/86Sr isotope ratios of each of them are measured. If the representative points lie in a straight line, the slope of the straight line is equal to (expλt -1) and the age of the system of boxes can be calculated" [4]
The advantage of the isochron method is that if there is any contamination of the sample over time, then the sample points will not be colinear, and the method is invariant of the amount of daugher radiometric element at time zero.
The Age of the Earth
Having outlined some of the basic principles behind radiometric dating, it's time to move to the question of the age of the Earth. The rocks dating from the formation of the Earth have long been recycled. Having said that, the oldest remaining rocks are close to 4000 million years old. As geologist G.B. Dalrymple points out:
The Amitsoq Gneisses in western Greenland, for example, have been dated by five different methods; within the analytical uncertainties, the ages are the same and indicate that these rocks are about 3.7 billion years old. [5]
This lower bound of the age of the Earth based on direct measurement of the age of the oldest rocks alone gives a figure several orders of magnitude higher than that of the YEC claim. Furthermore, given that five different dating methods give roughly the same figure, it is stretching credulity to argue that the dating methods are unreliable. If they were, one would hardly expect multiple independent methods to converge on the same figure.
It we assume (quite reasonably) that the Earth, moon, and meteorites will have formed at the same time, then measuring the ages of the latter two should give ages that are roughly equal, and therefore provide a measure for the age of the Earth. Dalrymple notes that some of the least disturbed stone meteorites are around 4500 to 4700 thousand million years old, while some of the oldest moon rocks are around 4500 million years old. Again, this convergence of values is hard to dismiss as coincidence.
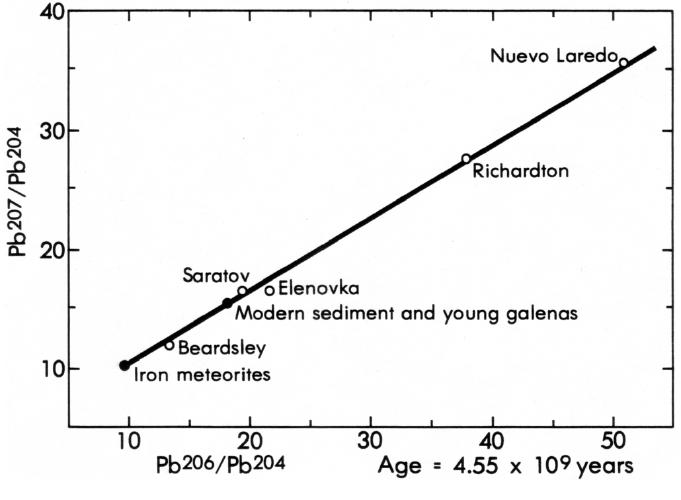
As for how we've determined the age of the Earth, Dalrymple notes:
The generally accepted age of the Earth is based on a simple but elegant model for the evolution of lead isotopes. This model was developed independently by Houtermans and Holmes, and first applied to meteorites and the Earth by Clair Patterson, now at the California Institute of Technology, in 1953. In his classic paper, Patterson reasoned that if the Pb-isotopic composition were uniform in the solar nebula and, thus, uniform in the planetary bodies and meteorites at the time of their formation, and if these bodies contained differing amounts of uranium, then the Pb-isotopic composition of these bodies should fall on a straight-line isochron when the 207Pb/204Pb ratio is plotted against the 206Pb/204Pb ratio (Figure 8). The lower end of the isochron in Figure 8 represents the Pb-isotopic composition in a phase of iron meteorites (troilite, or iron sulfide) that contains no uranium; this point represents the initial Pb-isotopic composition of the Solar System.
The Pb-isotopic compositions of iron and stone meteorites fall on an isochron age of 4.55 billion years (Figure 8). Note that this method, like the other isochron methods, is self-checking. Modern Earth leads, as represented by the Pb-isotopic compositions of some very young non-uranium-bearing minerals, also fall close to the meteoritic isochron, a result that we would expect if the Earth and meteorites formed contemporaneously. The ratios in lunar rocks have much larger values than those in terrestrial rocks and meteorites; they fall out of the field of Figure 8, but they do lie very close to the extension of the meteoritic isochron and, therefore, indicate a similar age.
Figure 8: Meteoric lead-isotope isochron showing that the age of meteorites and the Earth is about 4.55 billion years. After Murthy and Patterson (98) and York and Farquhart (136).
If the Earth, the Moon, and meteorites were not genetically related and of the same age, there would be no reason for their Pb-isotopic compositions to lie along the same isochron. This is convincing evidence that the planetary bodies, including the Earth, all formed about 4.55 billion years ago. Note that Patterson’s original estimate of the age of the Earth has changed very little over the past three decades. In a recent reevaluation, Tera concludes that the age of the Earth is about 4.54 billion years. Tera also summarizes several other lead models for the Earth’s age; they all give results within the range 4.43 to 4.59 billion years. Thus, although there is still some debate about the exact age of the Earth and the Solar System, scientists are quibbling only about the first one- or two-tenths of a billion years. The age of the Earth is known to within about one part in 45, i.e., about two percent. (Emphasis mine) [6]
Conclusion
This post barely covers the subject, but should be enough to show that when a YEC layperson blithely asserts that the age of the Earth has not been reliably determined, and that the dating methods are unreliable, they making a wild claim which given their lack of expertise in geochronology alone automatically dismisses the likelihood of it being worth considering. None of this is intended to belittle, but point out a simple fact: a layperson making a sweeping statement about a scientific field in which they have no expertise is simply not going to be taken seriously.
As we've seen, with respect to the specific claim - the age of the Earth - even a casual review of the evidence is enough to show that the YEC claims are hardly reflected by the evidence, while the allegation that radiometric dating is unreliable owes more to wishful thinking than hard evidence. Unfortunately, experience has taught me that most of the YEC zealots are without insight into how poor their grasp of the scientific issues is. However, they are not the target. Rather, it is the average believer who may be at risk of confusing fervency of views held for veracity. The past three posts should remind them of the need to listen to those who know what they are talking about, and regard pronouncements by those speaking against a robust consensus who are not competent professionals in that area with scepticism at best.
References
1. Walker C.C., ‘The Age of the Earth’, The Christadelphian (1911) 48:450
2. Knödlseder, J. "Constraints on stellar yields and Sne from gamma-ray line observations." New Astronomy Reviews (2000) 44: 315-320.
3. Prantzos N "Gamma-Ray Line Astrophysics and Stellar Nucleosynthesis: Perspectives for INTEGRAL" (1999) arXiv:astro-ph/9901373v1
4. Allègre Isotope Geology (2008, Cambridge University Press) p 79
6. ibid